2017-05-18 21:02:59
目录
描述性分析
什么是描述性分析
- 统计分析包括统计描述(descriptive statistics)和统计推断(inferential statistics)
- 描述性统计: 定量描述/汇总一批样本资料
- 推断性统计: 利用样本信息推断总体特征
- 描述是推断的基础
- 描述性分析一般不涉及概率推断
一个外行拿到资料后首先会问的问题:
数据量多大? 平均多少?最大/最小是多少? 每个月分别多少? …
描述性分析的内容
- 定量(quantitative)数据
- 聚集趋势: 均数、中位数、众数、…
- 离散趋势: 标准差、方差、全距、…
- 定性(qualitative)数据
- 频数分布
- 频率分布
- 分布情况: 偏度、峰度
- 交叉表
聚集和离散趋势
聚集趋势
- 均数 (mean)
> mean(cars$speed) [1] 15.4
- 中位数 (median)
> median(cars$speed) [1] 15
- 分位数 (percentile)
> quantile(cars$speed, c(0, 0.05, 0.5, 0.95, 1)) 0% 5% 50% 95% 100% 4 7 15 24 25
聚集趋势 (续)
- 众数: R没有内建的众数函数,需要自定义
# 构建一个S3泛函数calcMode,调用通用方法"calcMode"
> calcMode <- function(x) UseMethod("calcMode")
> calcMode.default <- function(x) max(unique(table(x)))
> calcMode.list <- function(x) sapply(x, function(v) max(unique(table(v))))
> calcMode.data.frame <- calcMode.list
- 对于数据框和向量,调用不同的方法,输出不同的格式
> calcMode(cars)
speed dist
5 4
> calcMode(cars$speed)
[1] 5
离散趋势
- 标准差 (standard deviation)
> sd(cars$speed) [1] 5.287644
- 方差 (variance)
> var(cars$speed) [1] 27.95918
- 全距 (range)
> range(cars$speed) [1] 4 25
汇总描述
summary函数
> summary(cars$speed)
Min. 1st Qu. Median Mean 3rd Qu. Max.
4.0 12.0 15.0 15.4 19.0 25.0
Hmisc包的describe函数(更详尽)
> Hmisc::describe(cars$speed)
cars$speed
n missing distinct Info Mean Gmd .05 .10 .25 .50 .75 .90 .95
50 0 19 0.996 15.4 6.077 7.0 8.9 12.0 15.0 19.0 23.1 24.0
Value 4 7 8 9 10 11 12 13 14 15 16 17 18 19 ...
Frequency 2 2 1 1 3 2 4 4 4 3 2 3 4 3 ...
Proportion 0.04 0.04 0.02 0.02 0.06 0.04 0.08 0.08 0.08 0.06 0.04 0.06 0.08 0.06 ...
分布情况
偏度和峰度
- 偏度: R并不自带偏度函数,可加载
e1071包
> e1071::skewness(cars$dist) [1] 0.7591268 # >0,右偏
- type = 3
- \(g_1 = m_3 / m_2^ {3/2}\). 经典方法
- \(G_1 = G_1 = g_1 \sqrt{n(n-1)} / (n-2)\). SAS和SPSS
- \(b_1 = m_3 / s^3 = g_1 ((n-1)/n)^ {3/2}\). MINITAB和BMDP
- 峰度: R并不自带峰度函数,可加载
e1071包
> e1071::kurtosis(cars$speed) [1] -0.6730924 # <0,峰不太陡峭(较正态分布更缓)
- type = 3
- \(g_2 = m_4 / m_2^2 - 3\). 经典方法
- \(G_2 = ((n+1) g_2 + 6)(n-1)\) \(/((n-2)(n-3))\). SAS和SPSS
- \(b_2 = m_4 / s^4 - 3\) \(= (g_2 + 3)(1 - 1/n)^2 - 3\). MINITAB和BMDP
直方图
- 绘制直方图,快速判断分布特征
hist()
hist(cars$dist)
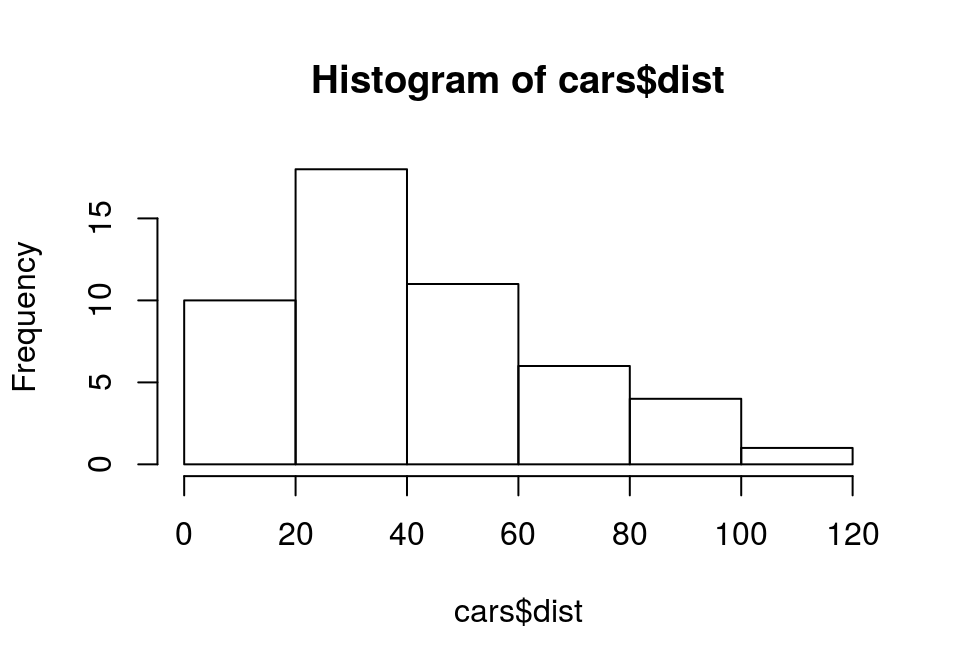
hist(cars$speed)
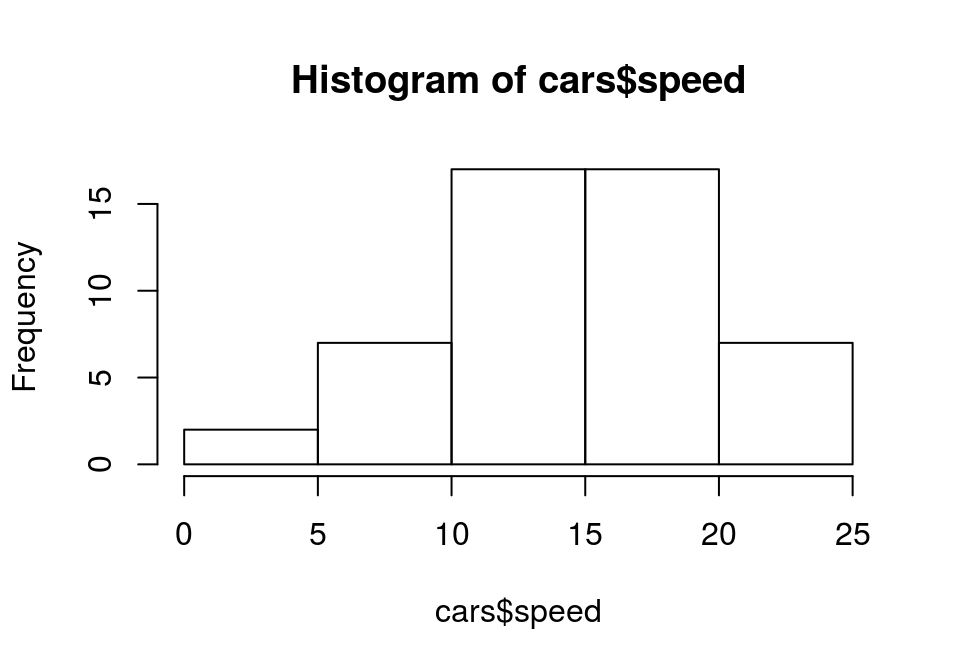
频数分布
简单频数/率表: table和prop.table函数
- 一维对象
> table(mtcars$gear)
3 4 5
15 12 5
> prop.table(table(mtcars$gear))
3 4 5
0.46875 0.37500 0.15625
- 多维对象
> table(mtcars[,c("am", "carb")])
carb
am 1 2 3 4 6 8
0 3 6 3 7 0 0
1 4 4 0 3 1 1
交叉频数表: ftable函数
- 明细表: 频数
> ftable(mtcars[, c("gear", "am", "vs")], row.vars="gear", col.vars=c("am", "vs"))
am 0 1
vs 0 1 0 1
gear
3 12 3 0 0
4 0 4 2 6
5 0 0 4 1
- 汇总矩阵: 求和
> ftable(Titanic, row.vars=1, col.vars=c(2,4))
# 如果是ftable(as.data.frame(Titanic), row.vars=1, col.vars=c(2,4))呢?
Sex Male Female
Survived No Yes No Yes
Class
1st 118 62 4 141
2nd 154 25 13 93
3rd 422 88 106 90
Crew 670 192 3 20
进阶交叉汇总: xtabs函数
xtabs交叉,as.data.frame.table还原
> xtabs(Freq ~ Gender + Admit, as.data.frame(UCBAdmissions))
Admit
Gender Admitted Rejected
Male 1198 1493
Female 557 1278
> xtabs(cbind(ncases, ncontrols) ~ agegp, data = esoph)
agegp ncases ncontrols
25-34 1 116
35-44 9 199
45-54 46 213
55-64 76 242
65-74 55 161
75+ 13 44
> as.data.frame.table(xtabs(Freq ~ Gender + Admit, as.data.frame(UCBAdmissions))) Gender Admit Freq 1 Male Admitted 1198 2 Female Admitted 557 3 Male Rejected 1493 4 Female Rejected 1278
一些实用统计函数
- 行计算:
rowSums,rowMeans
> m <- xtabs(Freq ~ Gender + Admit, as.data.frame(UCBAdmissions)) > rowSums(m) Male Female 2691 1835 > rowMeans(m) Male Female 1345.5 917.5
- 列计算:
colSums,colMeans
> colSums(m)
Admitted Rejected
1755 2771
> colMeans(m)
Admitted Rejected
877.5 1385.5
- 累加:
cumsum
> cumsum(1:10) [1] 1 3 6 10 15 21 28 36 45 55
完整的频数统计表
- 由明细记录表开始
> t1 <- ftable(mtcars[, c("gear", "vs", "am")], row.vars=1:2, col.vars=3)
> t1
am 0 1
gear vs
3 0 12 0
1 3 0
4 0 0 2
1 4 6
5 0 0 4
1 0 1
- 频率统计
> t2 <- prop.table(t1)
> t2
am 0 1
gear vs
3 0 0.37500 0.00000
1 0.09375 0.00000
4 0 0.00000 0.06250
1 0.12500 0.18750
5 0 0.00000 0.12500
1 0.00000 0.03125
完整的频数统计表 (续)
- 合并频率和频数
> t3 <- cbind(t1, t2) > t3 <- t3[, c(seq(1, 4, by=2), seq(2, 4, by=2))]
- 定义ftable属性
> t3 <- structure(t3, class='ftable', row.vars=attr(t1, "row.vars"),
+ col.vars=attr(t1, "col.vars"))
> attr(t3, 'col.vars')$stat <- c("Freq", "Pct")
> t3
am 0 1
stat Freq Pct Freq Pct
gear vs
3 0 12.00000 0.37500 0.00000 0.00000
1 3.00000 0.09375 0.00000 0.00000
4 0 0.00000 0.00000 2.00000 0.06250
1 4.00000 0.12500 6.00000 0.18750
5 0 0.00000 0.00000 4.00000 0.12500
1 0.00000 0.00000 1.00000 0.03125
完整的频数统计表 (续)
- 另一个办法是
dcast
> t4 <- data.table::dcast(mtcars, gear+vs ~ am, fun=length, value.var="am",
+ margins=c("am", "gear")) # 获得频数统计
> t4[, c("%_0", "%_1")] <- rbind(prop.table(t4[1:6, 3:4]),
+ prop.table(t4[7, 3:4])) # 获得频率统计
> t4[, "%_all"] <- rowSums(t4[, 6:7]) # 计算合计
> t4[, 6:8] <- sapply(t4[,6:8], function(v) {
+ sprintf("%3.2f%%", 100*v)}) # 格式转换(百分比)
> t4
gear vs 0 1 (all) %_0 %_1 %_all
1 3 0 12 0 12 37.50% 0.00% 37.50%
2 3 1 3 0 3 9.38% 0.00% 9.38%
3 4 0 0 2 2 0.00% 6.25% 6.25%
4 4 1 4 6 10 12.50% 18.75% 31.25%
5 5 0 0 4 4 0.00% 12.50% 12.50%
6 5 1 0 1 1 0.00% 3.12% 3.12%
7 (all) (all) 19 13 32 59.38% 40.62% 100.00%
交叉表
交叉和堆积
- 在数据变形部分,曾介绍过熔解
melt和重铸cast - 熔解(堆积)的目的是得到单向表 (长表 long table)
- 最简单的: 键值对
- 常见的: 复合多属性列的数值列
- 重铸(交叉)的目的是获得可建模的多维表,或汇总统计 (宽表 wide table)
- 日常接触的多数表格都是多维的
- Excel的数据透视表(pivot table)是典型的重铸汇总表
- 实际使用中,单向表和多维表的概念是相对的
数据结构
- 单向表是分析的基石
- 单向明细表本身就是关系型数据库理想的表设计范式
- 建议以单向明细表存储、交换数据
- 在索取原始数据时,单向明细表是最优选择
- 有了单向明细,再交叉计算结果
- 不要急于交叉,交叉的过程往往损失信息
> as.data.frame(t2) gear vs am Freq 1 3 0 0 0.37500 2 4 0 0 0.00000 3 5 0 0 0.00000 4 3 1 0 0.09375 ... 9 5 0 1 0.12500 10 3 1 1 0.00000 11 4 1 1 0.18750 12 5 1 1 0.03125
Thank you!